Description of the Point Cover Algorithms
- Date 20/07/2017.
- Author: Guillaume Touya
- Contact {firstname.lastname}@ign.fr.
Description of the algorithm
The Point Cover algorithm replace a point cloud by polygons that cover the region occupied by clusters of the points. First clusters have to be computed, using any of the available techniques. Then, a Delaunay Triangulation of the geographic object is created, and the longest segments (and their associated triangles) on the boundary of the hull are eliminated one by one, in order to reduce its spatial shape to the very structure of the points of the object. The algorithm stops in 4 cases:
- a point is put outside of the hull
- the hull is not regular anymore (ie. contains bridging edges)
- the hull doesn’t satisfy Jordan criteria anymore (ie. contains bridging points)
- minimal edge length removal is reached
The initial paper from Duckham & Galton describing the Delaunay based concave hull can be found here
| Parameter name | Description | Type | Default value |
|---|---|---|---|
| minLength | the minimal length of a triangulation segment to be kept as the outline of the hull | double (meters) |
Examples of generalization
Below, a set of points representing shipwrecks covered with the Delaunay concave hull of the clusters.

Below, a set of points representing shipwrecks covered with the convex hull of the clusters.
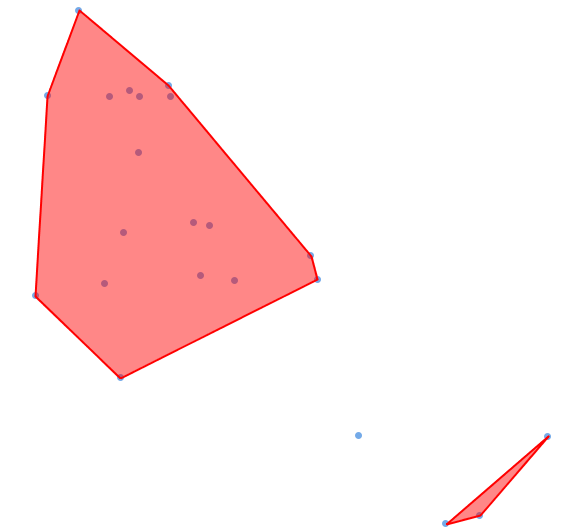
When to use the algorithm?
The algorithm tends to unsmooth geographic lines, and is rarely used to simplify geographic features. But it can be very useful to quickly filter the vertices of a line inside another algorithm.