Description of Raposo Hexagon Based Line Simplification Algorithm
- Date 20/07/2017.
- Author: Guillaume Touya
- Contact {firstname.lastname}@ign.fr.
Description of the algorithm
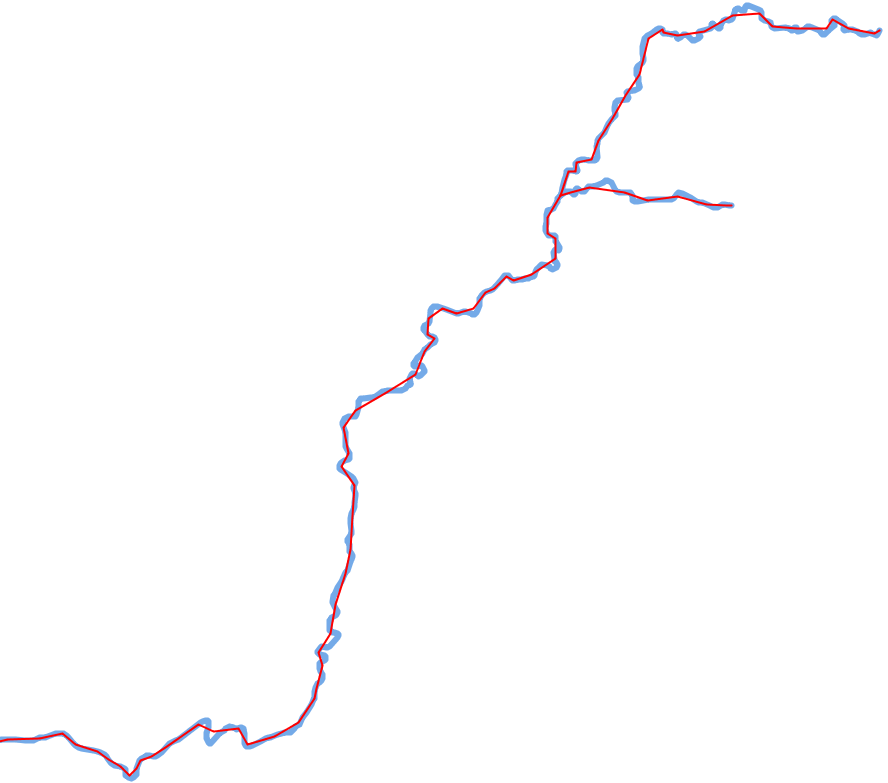
This algorithm simplifies lines based on a hexagonal tessallation, and is described in (Raposo 2013). The algorithm also works for the simplification of the border of a polygon object.
The idea of the algorithm is to put a hexagonal tessallation on top of the line to simplify, the size of the cells depending on the targeted granularity of the line. Similarly to the Li-Openshaw algorithm, only one vertex is kept inside each cell. This point can be the centroid of the removed vertices, or a projection on the initial line of this centroid. The shapes obtained with this algorithm are less sharp than the ones obtained with other algorithms such as Douglas-Peucker.
| Parameter name | Description | Type | Default value |
|---|---|---|---|
| use_method_1 | if true, uses the center of the hexagonal cells as new vertex, if false, the center is projected on the nearest point in the initial line | boolean | true |
| use_tobler_resolution | compute cell resolution based on Tobler’s formula if true, Raposo’s formula if false | boolean | true |
| initial_scale | the initial scale of the data (25000.0 for 1:25000 scale) | double |
Tobler based formula to compute hexagonal cell size: cell_size = 5 x l x s where l is the width of the line in the map in meters e.g. 0.0005 for 0.5 mm, and s is the target scale denominator.
Raposo’s formula to compute hexagonal cell size: cell_size = l / n x t / d where l is the length of the line, n the number of vertices of the line, t the denominator of the target scale, and d the denominator of the initial scale
Examples of generalization
When to use the algorithm?
The algorithm is dedicated to the smooth simplification of natural features such as rivers, forests, coastlines, lakes.