Moindres carrés génériques

Introduction

Le package leastsquaresgeneric du module geoxygene-contrib regroupe les algorithmes génériques (linéaires et non linéaires) de l’estimateur des moindres carrés.

Les calculs sont effectués à partir :

• des expressions algébriques des contraintes
• des noms des inconnues à estimer
• des paramètres de calcul

La généricité des algorithmes nécessite en contre-partie de considérer une équation linéaire comme un cas particulier d’équation non-linéaire. La résolution est alors effectuée suivant l’algorithme itératif de Gauss-Newton (généralisation de la méthode de Newton-Raphson aux systèmes d’équations).

Note importante : la dérivation numérique est calculée par une approximation (au mieux limitée à l’ordre 4). En fonction du conditionnement de la matrice N et de l’amplitude des erreurs introduites par la dérivation numérique, la résolution des équations normales peut conduire à des résultats aberrants. De même, dans certains cas, un système d’équations valides (dont une solution au sens des moindres carrés peut être trouvée en théorie) peut conduire dès les premières itérations à l’obtention d’une matrice singulière. Pour l’instant, le calcul étant réalisé avec la décomposition LU de la bibliothèque Jama, il pourrait être intéressant d’essayer de limiter la propagation des erreurs de dérivation numérique avec la décomposition QR de la bibliothèque Common-maths .

Package leastsquaresgeneric

Figure 1 - Diagramme des principales classes du package leastsquaresgeneric

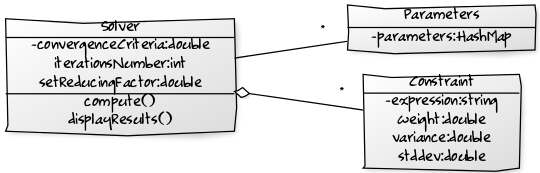
L’objet principal du package est le Solver :

Solver solver = new Solver();

L’intérêt principal du package est de pouvoir exprimer directement les contraintes sous forme algébrique (langage proche de Matlab) en chaine de caractères. Par exemple, pour définir une contrainte linéaire en x et y :

Constraint c1 = new Constraint("2*x + 3*y = 5");

Attention : les expressions algébriques ne doivent contenir que des valeurs numériques (constantes) ou des paramètres à estimer (variables inconnues du problème). Le code ci-dessous est utilisé pour insérer des identificateurs Java dans l’expression des contraintes.

double coeff1 = 2.0;
double coeff2 = 3.0;

Constraint c1 = new Constraint(coeff1 + "*x + " + coeff2 + "*y = 2");

Dans un deuxième temps, il est possible d’affecter des poids d’influence (ou directement des variances ou des écarts-types) aux différentes contraintes :

c1.setWeight(4.0);

// Ou de manière équivalente
c1.setVariance(0.25);
c1.setStddev(0.5)

Les contraintes sont alors ajoutées au Solver (ordre indépendant) :

solver.addConstraint(constraint);

Puis chaque variable utilisée dans les contraintes doit être déclarée dans le solver et être munie d’une valeur initiale (valeur approchée) :

solver.addParameter("x", 1);
solver.addParameter("y", 1);

Les paramètres sont alors choisis (certains sont optionnels). On peut définir entre autres les critères d’arrêts de l’algorithme. Dans le code ci-dessous, on spécifie un nombre maximal d’itérations à 100, mais l’algorithme pourra terminer plus tôt si l’incrément sur toutes les variables entre deux itérations est inférieur à 0.01 (par défaut, ces deux paramètres sont fixés à 0, ce qui signifie qu’ils doivent impérativement être spécifiés).

// Critère de convergence
solver.setConvergenceCriteria(0.01)

// Sécurité en cas de non convergence
solver.setIterationsNumber(100);

Il est également possible de définir les options de dérivation, i.e. le pas (0.1 par défaut) et l’ordre (2 par défaut) de dérivation :

// Pour une dérivation plus fine
solver.setDerivationStep(0.01);
solver.setDerivationOrder(4);

Enfin, un paramètre qui peut jouer un rôle important en cas de non convergence de l’algorithme : le facteur de réduction (qui réduit l’incrément entre deux itérations).

// Pour une dérivation plus fine
solver.setreducingFactor(0.1);

Le calcul peut alors être lancé :

solver.compute();

La fonction displayResult() permet un affichage standardisé des résultats obtenus.

solver.displayResults();

Sinon, la fonction getParameter() permet de récupérer les variables estimées. A noter qu’un paramètre peut-être adressé par son nom ou par un index (ordre d’insertion dans le Solver). Ainsi, le code suivant permet d’afficher l’ensemble des paramètres estimés avec les noms associés, indépendamment du code qui précède :

// Affichage personnalisé des résultats

System.out.println(solver.getEffectiveIterationsNumber() + " itérations ont été effectuées");
System.out.println("Les paramètres estimés sont : ")

for (int i=0; i<solver.getParametersNumber(); i++) {
  System.out.println(solver.getParameterName(i)+" = "+solver.getParameter(i))
}

Exemples d’utilisation

Estimation d’une fonction de transformation

Cette application est tirée du livre “Estimation par moindres carrés” (collection ENSG), page 172. L’objectif est de déterminer les paramètres de transformation entre deux jeux de données dont on connaît trois points d’appuis :

	x1 (jeu 1)	y1 (jeu 1)	x2 (jeu 2)	y2 (jeu 2)
Point 1	0.32	1.50	261 000	608 000
Point 2	0.15	1.25	256 000	604 000
Point 3	1.02	0.75	275 000	589 000

Par ailleurs, on nous informe que le rapport d’échelle pour passer du jeu 1 au jeu 2 est de l’ordre de 1/20 000e tandis que l’angle de rotation est proche de 5° (~ 0.1 rad), ce qui va permettre de donner une valeur approchée au vecteur de paramètres à estimer.

Le modèle de transformation utilisé est un modèle à 4 paramètres (Tx, Ty, k et θ). L’équation de changement de repère pour un point (x1,y1) s’écrit :

\[x2 = Tx + k*cos(θ)*x1 + k*sin(θ)*y1\]\[y2 = Ty - k*sin(θ)*x1 + k*cos(θ)*y1\]

On donne ci-dessous le code Java permettant de résoudre ce problème :

// Expression algébrique des 6 constraintes
Constraint c11 = new Constraint("Tx + k*cos(theta)*0.32 + k*sin(theta)*1.50 = 261000");
Constraint c12 = new Constraint("Ty - k*sin(theta)*0.32 + k*cos(theta)*1.50 = 608000");
Constraint c21 = new Constraint("Tx + k*cos(theta)*0.15 + k*sin(theta)*1.25 = 256000");
Constraint c22 = new Constraint("Ty - k*sin(theta)*0.15 + k*cos(theta)*1.25 = 604000");
Constraint c31 = new Constraint("Tx + k*cos(theta)*1.02 + k*sin(theta)*0.75 = 275000");
Constraint c32 = new Constraint("Ty - k*sin(theta)*1.02 + k*cos(theta)*0.75 = 589000");

Solver solver = new Solver();

// Ajout des contraintes
solver.addConstraint(c11);
solver.addConstraint(c12);
solver.addConstraint(c21);
solver.addConstraint(c22);
solver.addConstraint(c31);
solver.addConstraint(c32);

// Déclaration des 4 paramètres à estimer avec valeurs approchées
solver.addParameter("Tx", 20000);
solver.addParameter("Ty", 50000);
solver.addParameter("k", 20000);
solver.addParameter("theta", 0.1);

// Paramétrage des critères d'arrêt
solver.setIterationsNumber(100);
solver.setConvergenceCriteria(0.001);

solver.compute();

// Affichage des résultats
System.out.println("Apres "+solver.getEffectiveIterationsNumber()+" iterations :");
System.out.println("Tx  = "+solver.getParameter("Tx")+" m");
System.out.println("Ty  = "+solver.getParameter("Ty")+" m");
System.out.println("k  = "+solver.getParameter("k"));
System.out.println("theta  = "+solver.getParameter("theta")*180/Math.PI+" deg");

Le résultat obtenu dans la console est :

-----------------------------
 After 4 iterations
-----------------------------
Tx  = 248716.4310955899 m
Ty  = 574847.5915941315 m
k  = 23436.514058778277
theta  = 7.890587680637035 deg

Interpolation d’une fonction

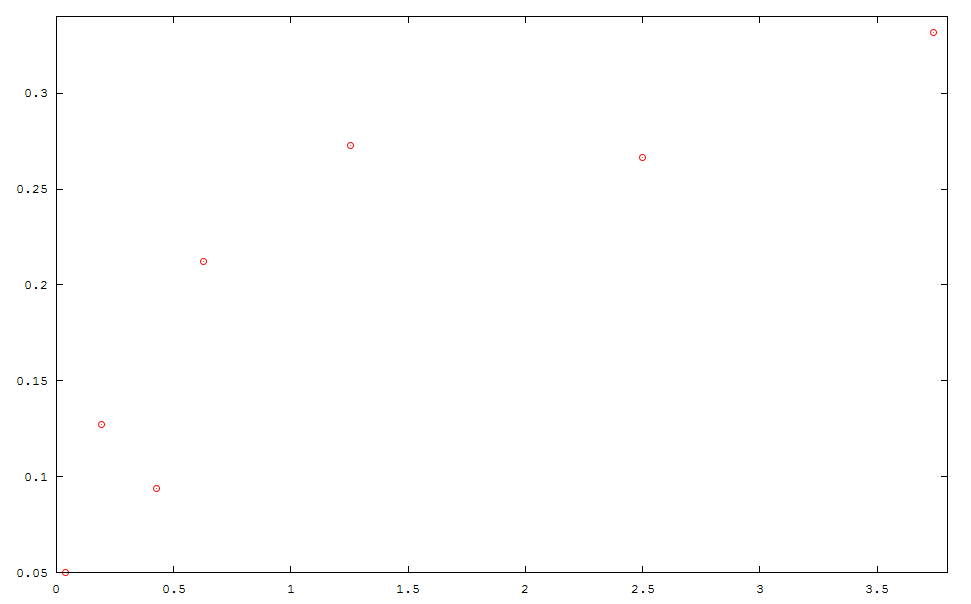
On considère le problème d’interpolation suivant :

Trouver les paramètres p1 et p2 de la fonction :

\[d(t) = (p1*t) / (p2*t+1)\]

permettant d’interpoler au mieux l’échantillon de point ci-dessous.

	1	2	3	4	5	6	7
t	0.038	0.194	0.425	0.626	1.253	2.500	3.740
d	0.050	0.127	0.094	0.212	0.273	0.267	0.332

Figure 2 - Représentation de l’échantillon des points

On donne dans un premier temps le code permettant de recréer les données :

ArrayList<Double> T = new ArrayList<Double>();
ArrayList<Double> D = new ArrayList<Double>();

T.add(0.038); D.add(0.050);
T.add(0.194); D.add(0.127);
T.add(0.425); D.add(0.094);
T.add(0.626); D.add(0.212);
T.add(1.253); D.add(0.273);
T.add(2.500); D.add(0.267);
T.add(3.740); D.add(0.332);

Puis le code permettant de trouver une estimation des paramètres de la fonction interpolante :

Solver solver = new Solver();

// Ajout des contraintes
for (int i=0; i<T.size(); i++){
  double t = T.get(i);
  double d = D.get(i);
  solver.addConstraint(new Constraint("p1*"+t+"/(p2*"+t+"+1) = "+d+""));
}

// Déclaration des inconnues
solver.addParameter("p1", 1);
solver.addParameter("p2", 1);

// Paramétrage du critère d'arrêt
solver.setIterationsNumber(10);
solver.setConvergenceCriteria(0.001);

// ----------------------------------
// Calculs et résultats
// ----------------------------------

solver.compute();

solver.displayResults();

On obtient les lignes suivantes dans la console :

-----------------------------
 After 6 iterations
-----------------------------
p1 = 0.6488940374077881
p2 = 1.7899669235296043

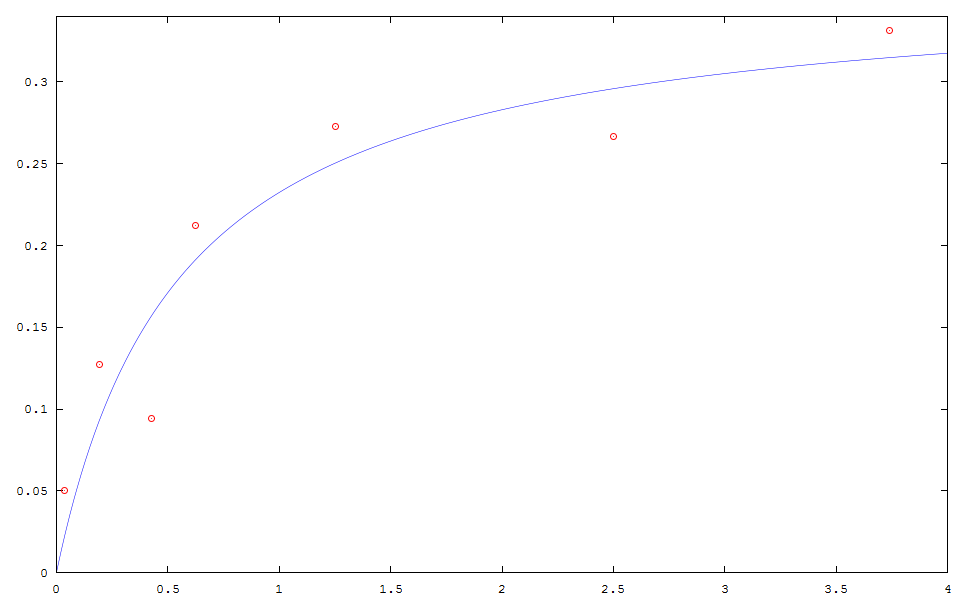
On peut alors tracer la fonction \(d(t) = (0.649t) / (1.790t + 1)\) sur l’échantillon de points :

Figure 3 - Estimation de la fonction d(t) d’interpolation

Contraintes impératives

Les contraintes impératives désignent l’ensemble des contraintes qui doivent être impérativement résolues. La solution retenue est alors la solution la plus proche des contraintes indicatives (au sens des moindres carrés) parmi l’ensemble des solutions qui vérifient ces contraintes impératives.

De manière très pragmatique, la gestion des contraintes impératives peut être implémentée simplement par une méthode de pondération forte. Ici, la méthode employée est celle des multiplicateurs de Lagrange, permettant d’aboutir à un résultat en théorie exact (aux erreurs de calcul près dans les cas non-linéaires) et qui ne soit pas tributaire des poids choisis. En revanche le nombre des contraintes de chaque type (impératif et indicatif) devra être en adéquation avec les nombre de paramètres à estimer.

Plus formellement, en notant ne le nombre d’équations de contraintes indicatives, nc le nombre de contraintes impératives et np le nombre de paramètres à estimer, une solution pourra être trouvées sous les deux conditions suivantes :

\[np ≤ ne + nc\]\[nc ≤ np\]

Une contrainte peut-être spécifiée comme étant impérative :

• Soit en deux temps, avec la méthode setImperative()

  Constraint c1 = new Constraint("2*x - y = 10");
  c1.setImperative(true);
  

• Soit en passant l’argument booléen _imperative_ dans le constructeur de contrainte

  Constraint c1 = new Constraint("2*x - y = 10", true);
  

• Soit directement par l’emploi du signe ”:=” dans l’expression algébrique de la contrainte

  Constraint c1 = new Constraint("2*x - y := 10");
  

Les méthodes de paramétrage, de lancement du calcul et de récupération des résultats restent inchangées par rapport au cas non contraint.

Exemple d’utilisation : On considère un triangle dont on a mesuré les trois angles : a = 60.27°, b = 40.54°, c = 83.12°. Le problème contraint s’exprime alors de la manière suivante :

Trouver une estimation des trois angles a, b et c sous la contrainte a + b + c = 180°

Le code Java correspondant est le suivant :

// Contraintes indicatives
Constraint c1 = new Constraint("a = 60.27");
Constraint c2 = new Constraint("b = 40.54");
Constraint c3 = new Constraint("c = 83.12");

// Contrainte impérative
Constraint c4 = new Constraint("a+b+c = 180", true);

Solver solver = new Solver();

solver.addConstraint(c1);
solver.addConstraint(c2);
solver.addConstraint(c3);
solver.addConstraint(c4);

// Valeurs initiales
solver.addParameter("a", 1);
solver.addParameter("b", 1);
solver.addParameter("c", 1);

solver.setIterationsNumber(5);

solver.compute();

solver.displayResults();

// On vérifie que la somme des angles vaut bien 180°
System.out.println("Somme des angles = "+(solver.getParameter("a")+solver.getParameter("b")+solver.getParameter("c")));

Le résultat retourné en console est alors :

-----------------------------
After 5 iterations
-----------------------------
a = 58.960000000000065
b = 39.23000000000006
c = 81.80999999999987
Somme des angles = 180.0

Dans notre cas de figure, l’estimation a simplement consisté à retrancher 1.31° (1/3 de l’excès par rapport à la valeur contrainte de 180°) sur chacun des angles. On remarquera que ce problème ne présente un réel intérêt pratique que lorsque les écart-types des mesures effectuées sur les angles sont sensiblement différents (cf partie suivante “indicateurs statistiques”) ou que les contraintes indicatives sont plus complexes que de simples affectations de variables.

Indicateurs statistiques

En règle générale, les méthodes et résultats qui suivent n’ont d’intérêt particulier que dans le cas ou les écart-types sur les mesures sont connus à l’avance (bien qu’il soit possible de les fixer “à l’aveugle” avant de les ré-estimer a posteriori avec le calcul du facteur unitaire de variance, cf plus loin).

Chaque équation est munie d’un poids correspondant :

Soit à un réel arbitraire :

constraint.setWeight(0.01);

Soit à l’inverse de son écart-type de mesure au carré (la fonction prend alors en entrée l’écart-type) :

constraint.setStddev(10);

Ou de manière équivalente, le raccourci “+/-” directement dans l’expression algébrique de la contrainte permet de spécifier +l’écart-type+ de l’observation :

Constraint constraint = new Constraint("2*x + 3*y = 113 +/- 10)

Soit à l’inverse de sa variance de mesure (la fonction prend alors en entrée la variance) :

constraint.setVariance(100);

Les indicateurs statistiques relatifs à l’estimation par moindres carrés peuvent être affichés dans la console à l’aide de la fonction displayFullResults() (version étendue de displayResults()). Les écart-types sur chaque paramètre estimé sont alors affichés avec le facteur unitaire de variance (pour la qualité globale de l’estimation) et les résidus (simples et normalisés).

solver.displayFullResults();

Ces résultats peuvent également être obtenus individuellement à l’aide des méthodes suivantes :

Méthodes de récupération des résidus (équations indicatives) :

• getResidual(int eq, int iteration) : récupération du résidu (non normalisé) de l’équation numéro eq à une itération donnée.
• getResidual(int eq) : récupération du résidu (non normalisé) de l’équation numéro eq après l’itération finale.
• getNormalizedResidual(int eq) : récupération du résidu normalisé de l’équation numéro eq après l’itération finale.
• getTotalResidual(int iteration) : récupération de la somme des résidus sur toutes les équations à une itération donnée.
• getMaxResidual(int iteration) : récupération du résidu maximal sur toutes les équations à une itération donnée.
• getTotalSquaredResidual(int iteration) : récupération de la somme des résidus au carré sur toutes les équations à une itération donnée.

Pour chaque équation, un résidu normalisé supérieur à 3 (sous l’hypothèse d’une distribution normale des erreurs de mesure) indique vraisemblablement une erreur de modèle, une mesure aberrante ou encore une erreur d’appréciation de l’écart-type sur la mesure.

Méthodes de récupération des variances d’estimation :

• getS02() : récupération du facteur unitaire de variance.
• getEstimationStd(int i) : récupération de l’écart-type d’estimation du paramètre i.
• getEstimationVariance(int i) : récupération de la variance d’estimation du paramètre i.
• getEstimationCovariance(int i, int j) : récupération de la covariance d’estimation des paramètre i et j.
• getEstimationCorrelation(int i, int j) : récupération du coefficient de corrélation entre les paramètre i et j.
• getEstimationStd(String si) : récupération de l’écrat-type d’estimation du paramètre de nom si.
• getEstimationVariance(String si) : récupération de la variance d’estimation du paramètre de nom si.
• getEstimationCovariance(String si, String sj) : récupération de la covariance d’estimation des paramètre de noms si et sj.
• getEstimationCorrelation(String si, String sj) : récupération du coefficient de corrélation entre les paramètre de noms si et sj.

Un facteur unitaire de variance élevé (relativement à l’unité) représente une erreur de modèle, des mesures aberrantes ou une sous-estimation des écart-types sur les mesures des grandeurs observées. Inversement, un facteur inférieur à 1 indique une sous-estimation de la précision des mesures en entrée.

Dans tous les cas, avant de décider de supprimer des mesures, il peut-être intéressant de relancer le calcul après avoir normalisé les variances de mesure par le facteur unitaire de variance (les résultats de l’estimation seront identiques mais les écart-types d’estimation et les résidus normalisés seront plus représentatifs).

Exemple complet

Dans cet exemple, on cherche à déterminer une estimation du centre et du rayon d’une distribution circulaire de points, dont l’observation des positions a été entachée d’une erreur de mesures.

Création du jeu de test

Dans un premier temps, simulons cette erreur de mesure. On considérera que le cercle solution est de rayon Rc = 80 m et est centré sur le point C avec Xc = 120.0 m et Yc = 50.0 m. On génère une série de points en coordonnées polaires par rapport au centre du cercle suivant deux lois uniformes en r et θ. Les coordonnées cartésiennes des points sont alors stockées dans deux tables X et Y. Soit N le nombre de points tirés.

// ------------------------------------------------------------
// Cercle solution
// ------------------------------------------------------------
double Xc = 120;
double Yc = 50;
double Rc = 80;
// ------------------------------------------------------------

// ------------------------------------------------------------
// Simulation de la mesure des points
// ------------------------------------------------------------
int N = 200;

ArrayList<Double> X = new ArrayList<Double>();
ArrayList<Double> Y = new ArrayList<Double>();

for (int i=0; i<N; i++) {
    double r = Rc + 3 * (Math.random() - 0.5) * Math.sqrt(12);
    double t = Math.random() * 2 * Math.PI;

    X.add(Xc + r * Math.cos(t));
    Y.add(Yc + r * Math.sin(t));
}

Remarquer que la loi uniforme sur r est prise d’amplitude égale à \(3 \sqrt{12}\), donnant ainsi à sa variable aléatoire associée un écart-type égal à 3.

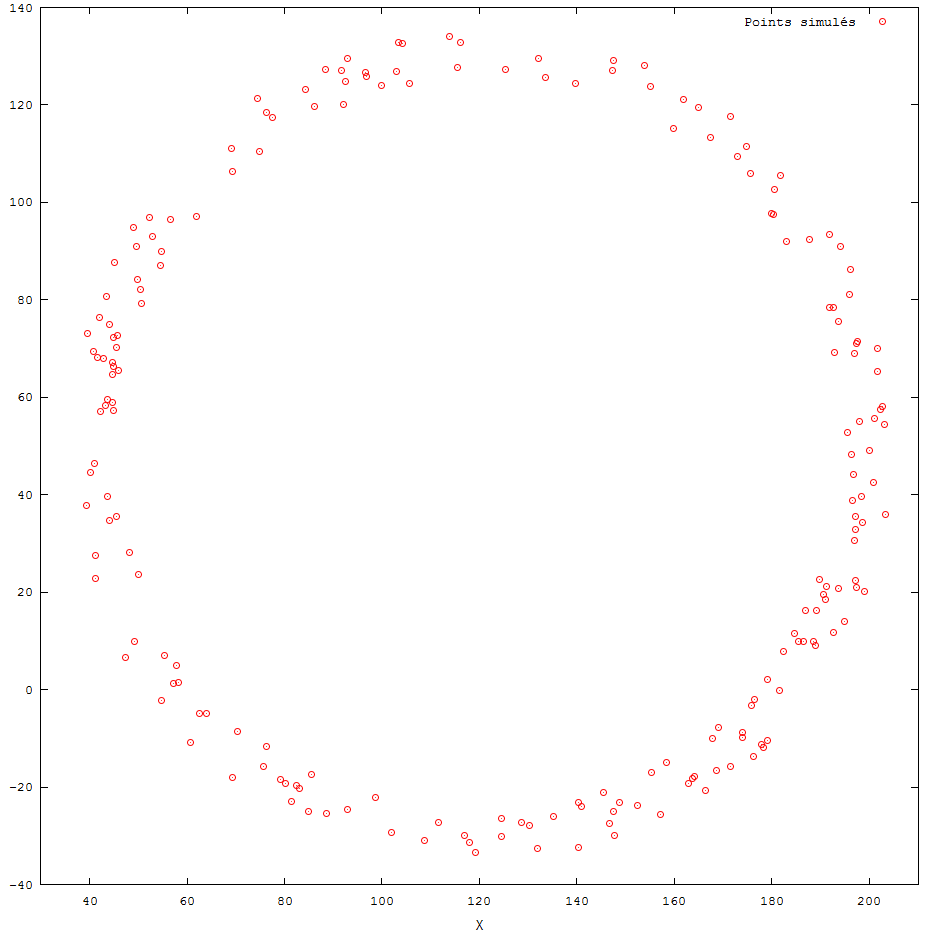
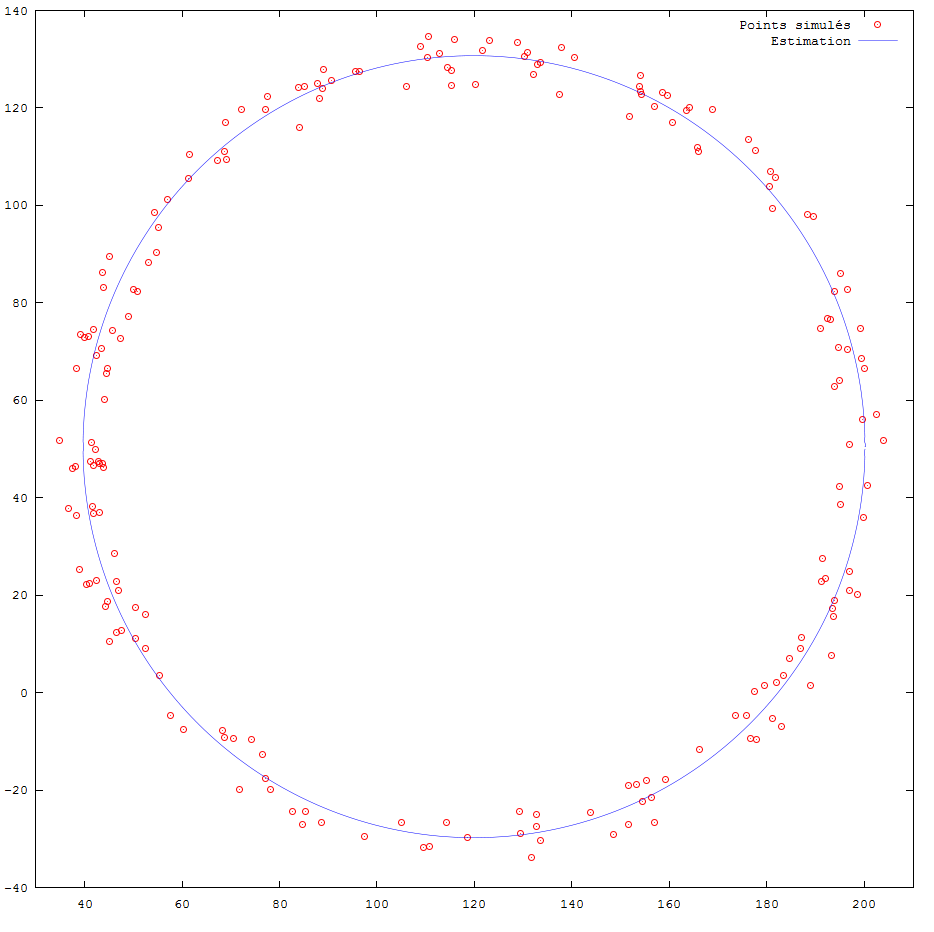
Ce qui donne :

Figure 4 - Courbe des observations simulées

Implémentation de la solution

Pour chaque point mesuré (x,y), l’équation d’observation associée s’exprime par :

\[(x-Xc)^2 + (y-Yc)^2 - Rc^2 = 0\]

Afin d’éviter d’obtenir une solution négative pour le rayon, il est préférable de prendre la racine carrée de cette équation.

Choisissons comme écart-type : 1m (correspondant au 3m pris dans la construction du jeu de test).

Le code suivant permet d’effectuer une estimation par moindres carrés des paramètres du cercle passant au mieux par les points simulés.

// ------------------------------------------------------------
// Estimation par moindres carrés
// ------------------------------------------------------------

Solver solver = new Solver();

for (int i=0; i<N; i++) {
    double x = X.get(i);
    double y = Y.get(i);

    solver.addConstraint(new Constraint("sqrt(("+x+"-Xc)^2 + ("+y+"-Yc)^2) - Rc = 0 +/- 1.0"));
}

solver.addParameter("Xc", 100);
solver.addParameter("Yc", 100);
solver.addParameter("Rc", 100);

solver.setIterationsNumber(10);

solver.compute();

// Affichage des résultats
solver.displayFullResults();

// Affichage des corrélations
System.out.println("Corrélations : ");
System.out.println("[Xc,Yc] : " + solver.getEstimationCorrelation("Xc", "Yc"));
System.out.println("[Xc,Rc] : " + solver.getEstimationCorrelation("Xc", "Rc"));
System.out.println("[Yc,Rc] : " + solver.getEstimationCorrelation("Yc", "Rc"));

// Récupération des paramètres estimés
double XcChap = solver.getParameter("Xc");
double YcChap = solver.getParameter("Yc");
double RcChap = solver.getParameter("Rc");

Les résultats retournés par la console sont alors (sans les résidus) :

// -----------------------------
//  Unit variance factor
// -----------------------------
s02 = 8.781224765741552
s0 = 2.9633131400075747
// -----------------------------
//  After 10 iterations
// -----------------------------
Xc = 120.00251244781892 +/- 0.28901794998945496
Yc = 50.024837173134486 +/- 0.30857385695135314
Rc = 79.6647544277168 +/- 0.2117827341653287

Correlations :
[Xc,Yc] : -0.04396946802433635
[Xc,Rc] : -0.11932157505562874
[Yc,Rc] : -0.07743568198742104

Remarquons :

1. On retrouve les paramètres (au cm près pour la position et 35 cm près pour le rayon) avec des écart-types d’estimation évalués à une trentaine de cm.
2. La racine du facteur unitaire de variance est proche de 3, correspondant à notre sous-estimation (volontaire pour l’exemple) d’un facteur 3 de l’écart-type sur les observations.
3. De manière plus anecdotique, les corrélations entre paramètres estimés sont quasi-négligeables.

Figure 5 - Estimation du cercle

Ajout d’une contrainte

Modifions l’ennoncé du problème en y ajoutant une contrainte supplémentaire, de type impérative (ici avec le symbole ”:=”). Ce problème devient un problème d’optimisation sous contrainte.

Pour cela, spécifions que le cercle doit impérativement passer par un point donné : (0,0) dans notre exemple.

solver.addConstraint(new Constraint("sqrt(Xc^2+Yc^2)-Rc := 0"));

Les résultats retournés sont alors :

// -----------------------------
//  Unit variance factor
// -----------------------------
s02 = 752.6993782519672
s0 = 27.435367288446628
// -----------------------------
// After 10 iterations
// -----------------------------
Xc = 88.31928892956398 +/- 1.7325705904573305
Yc = 36.73112200860588 +/- 2.5262655403439744
Rc = 95.6528730411946 +/- 1.4294983796618161

Correlations :
[Xc,Yc] : -0.4693535665330969
[Xc,Rc] : 0.8005732688257923
[Yc,Rc] : 0.15337866550455684

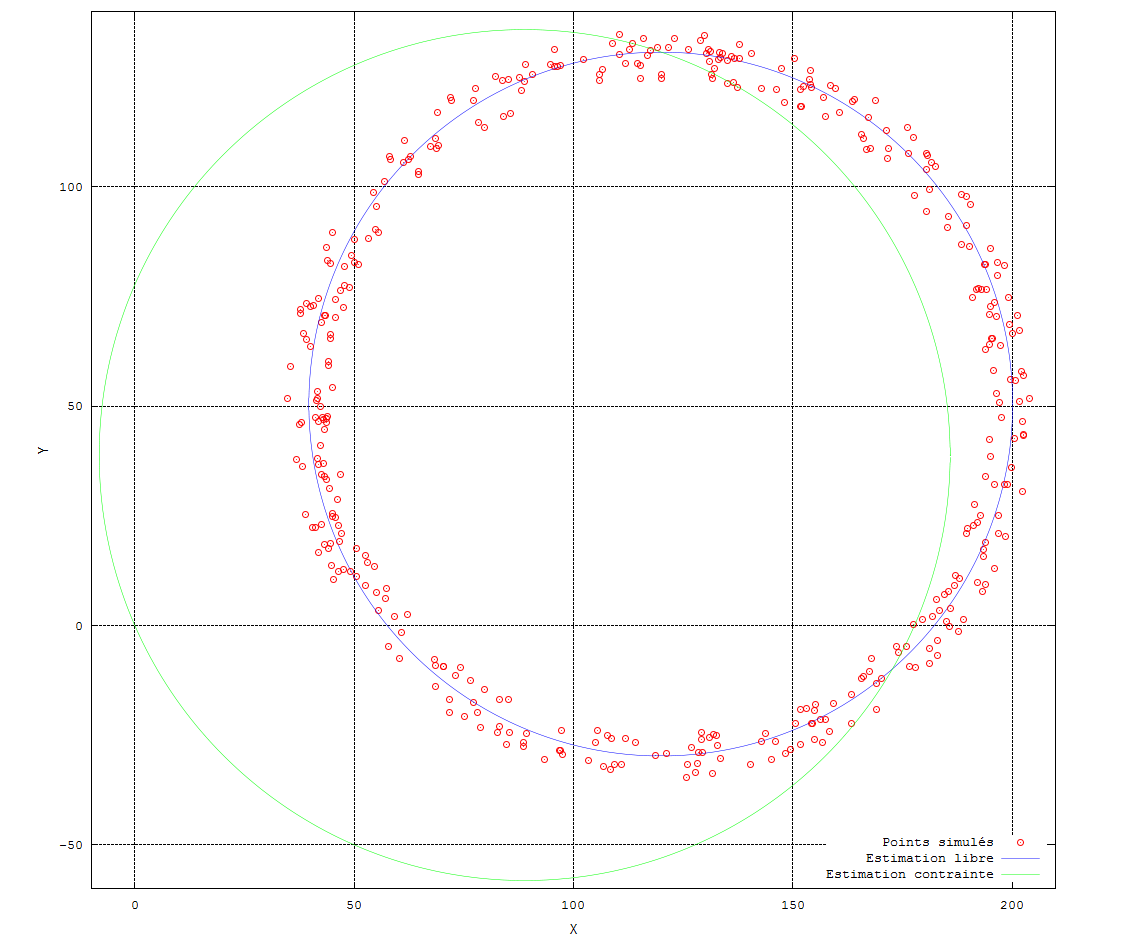
On remarque cette fois-ci que :

1. Les paramètres estimés sont plus éloignés de la vérité terrain (avec des écart-types associés plus importants).
2. Le facteur unitaire de variance est plus élevé que dans le cas libre, traduisant ici en particulier un problème de modèle (en pratique le cercle ne passe pas par l’origine, comme on peut le voir sur la figure ci-dessous).
3. Les corrélations entre paramètres ne sont plus négligeables (ce qui est naturel puisque, sachant à présent que le cercle doit passer par l’origine, plus le centre est loin de O, plus le rayon doit être important pour “compenser”. Si la contrainte était une relation explicite entre Xc et Yc par exemple, on aurait [Xc,Yc] ≈ 1;

Figure 6 - Estimation du cercle avec la nouvelle contrainte